The basics of data encryption with XOR by John Simons
XOR is still a widely used method for encryption, but: What is XOR? To understand this I first have to teach you something about ports.
Binary Port
I will show you by building up slowly the explanation of ports. First you have to understand what a port is. Well its not that difficult, a port is an input (like a switch) and an output (like a lamp). Just like the lightswitch in you're house, if you turn on the lightswitch, the lamp will go on. This is what we call a binary port, because the lamp is either on or off, it can not be a little bit on or almost "on" or a bit "off", because its on or off than, binary has only to states "on" or "off" also true or false, one or zero, 1 or 0 just look at this picture and you see what I mean: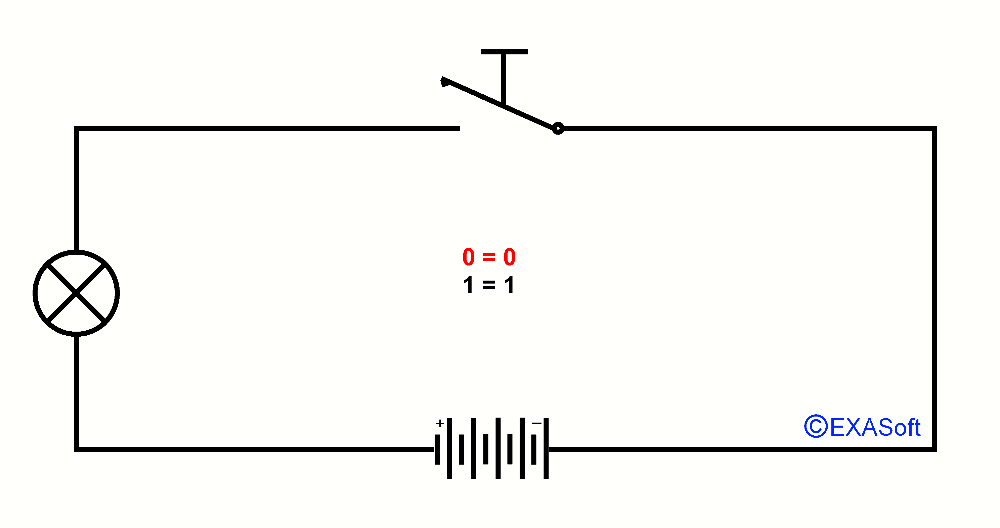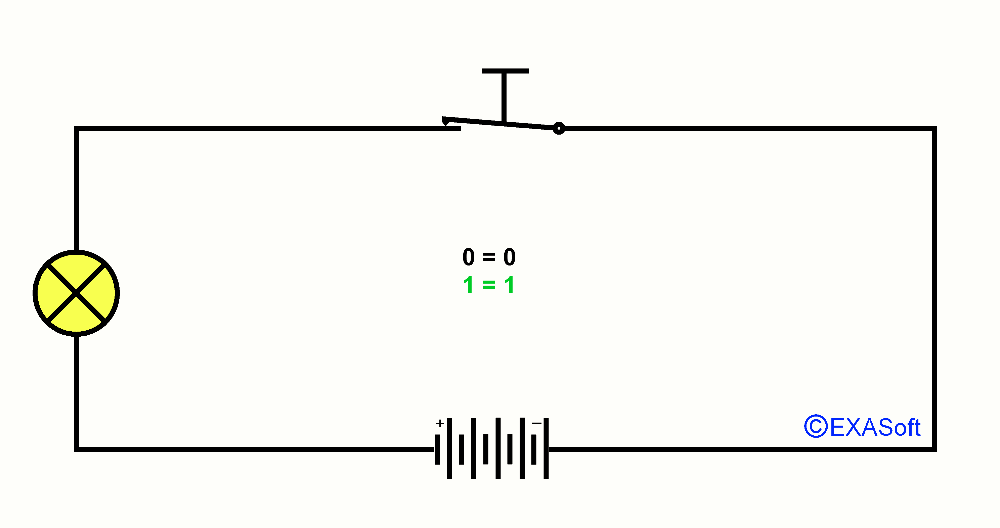
OR Port
Maybe you know the expression in the mathematics OR. OR is a logical operator, also called Boolean operator. Usually we use OR in a control statement. A practical example: You do not like sour apples and you also don’t like green apples: If (the Apple = sour) OR (the apple = green) than don’t eat it. In this case it doesn’t matter if the apple is green and sour, if both criteria match, the outcome is the same. So, this part was not very difficult was it? But we can do more with OR. lets say I have 2 switches that are parallel. Look at the picture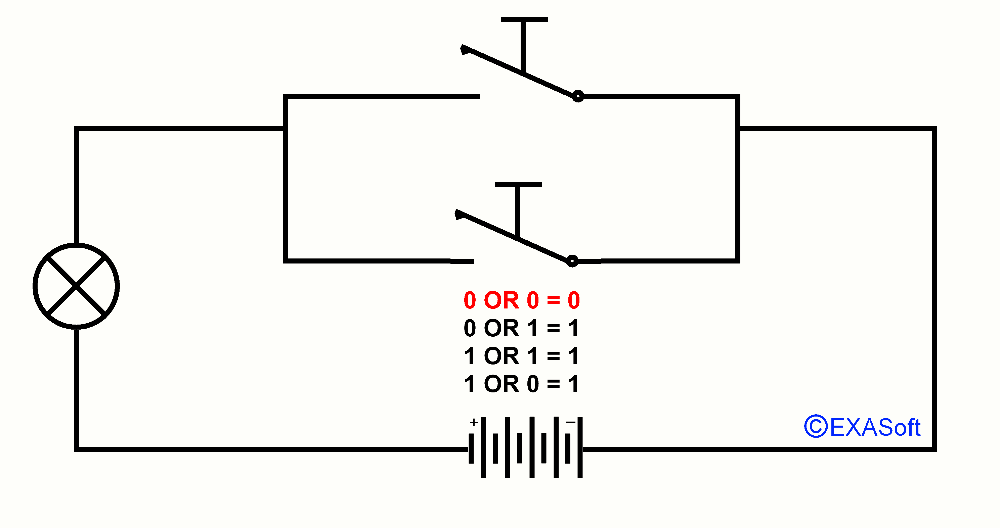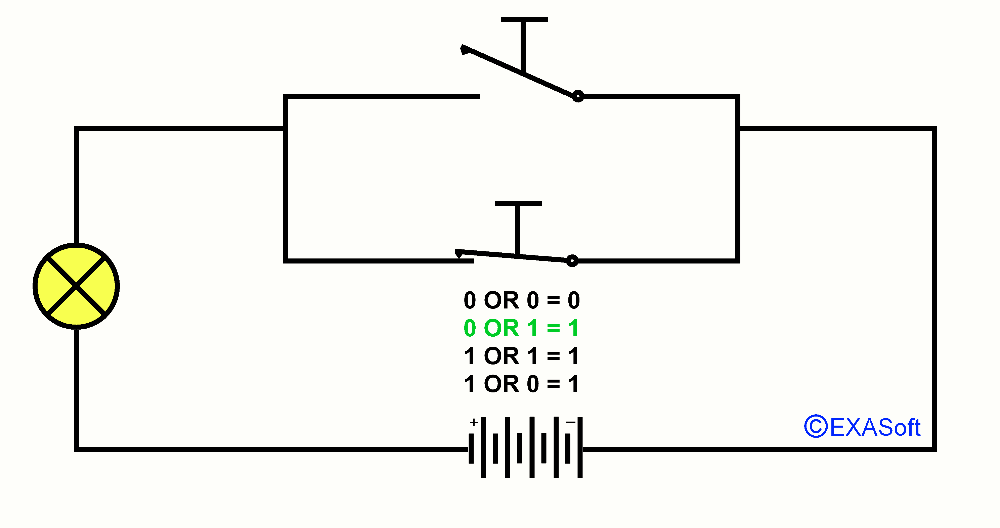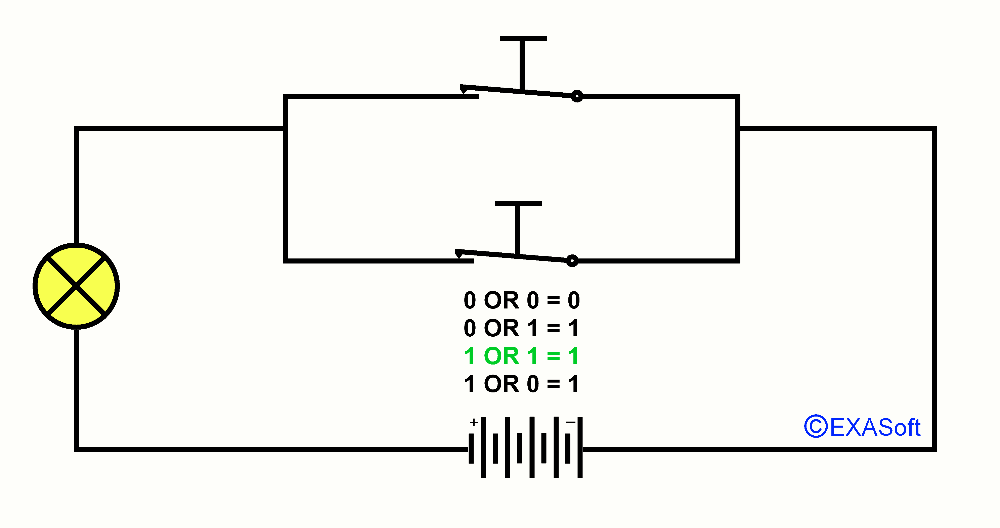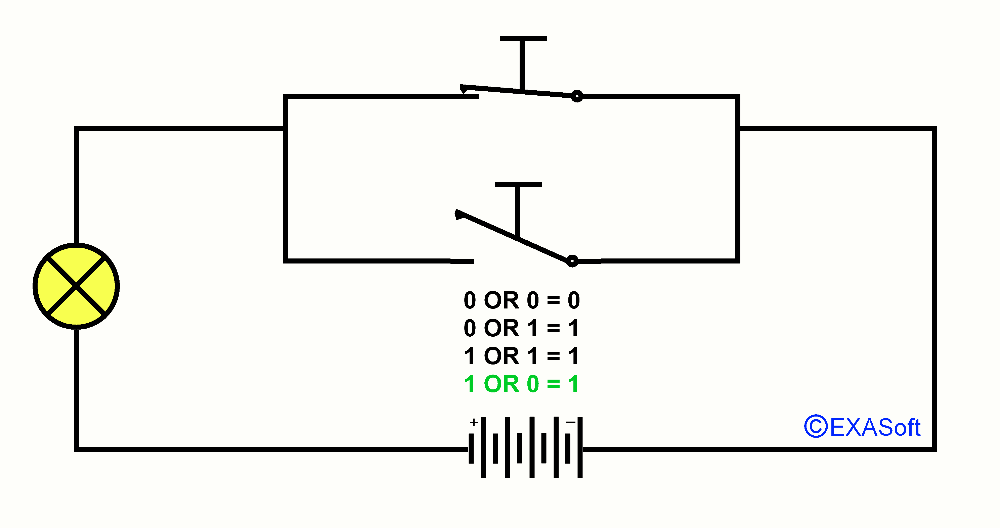
If switch 1 OR 2 is pressed down the lamp will turn on. We note the pressed switch as 1 and the not pressed switch as 0 the lamp if it is on the result returns 1 if it is off the result will be 0. You can then draw together the following table
0 OR 0 = 0
1 OR 0 = 1
0 OR 1 = 1
1 OR 1 = 1
AND Port
This way we also have an AND port, just look at the drawing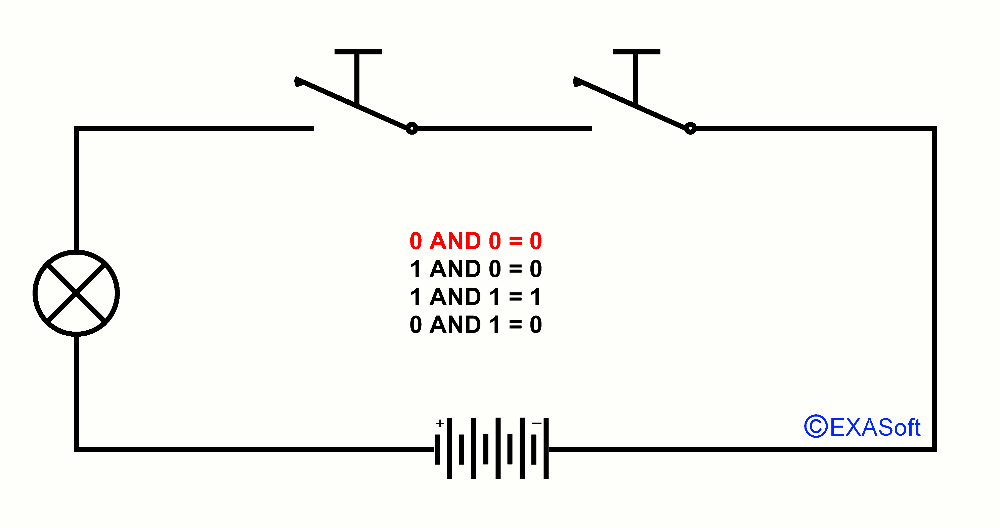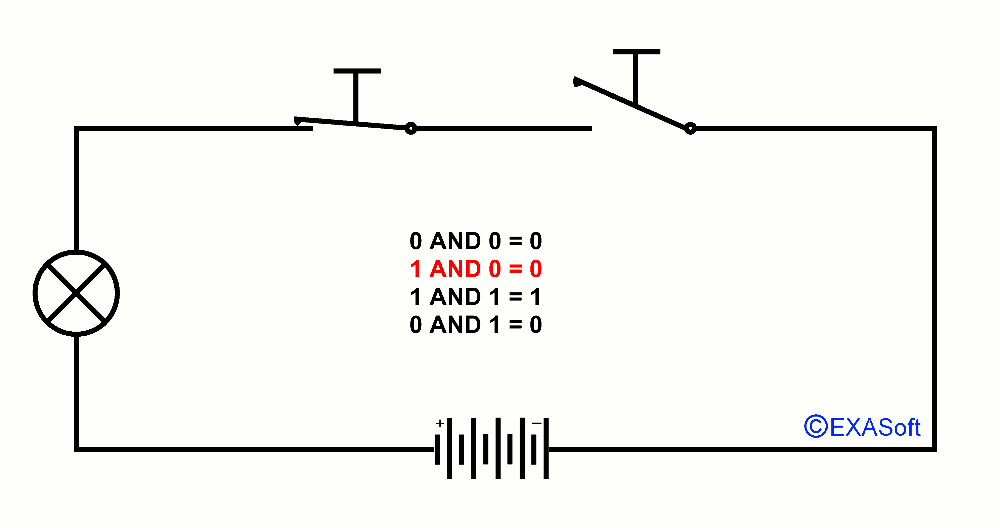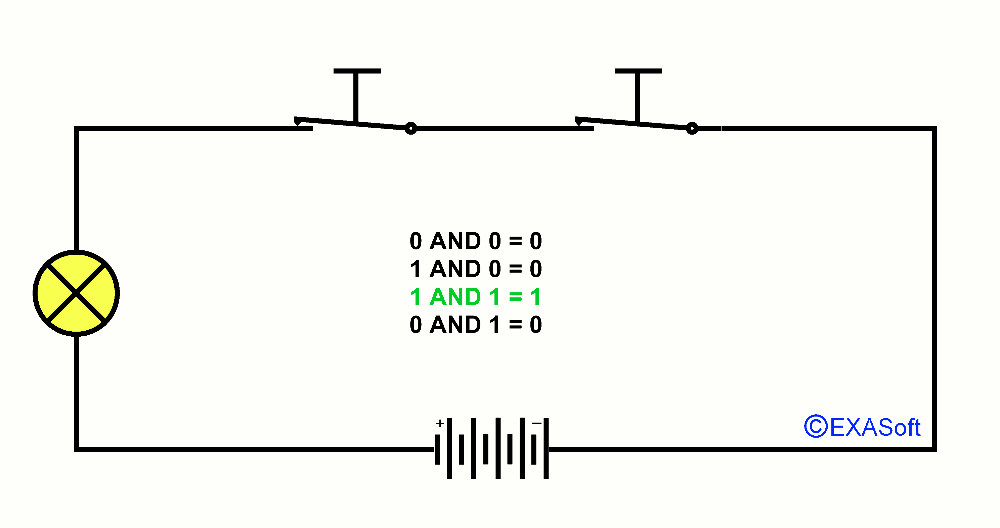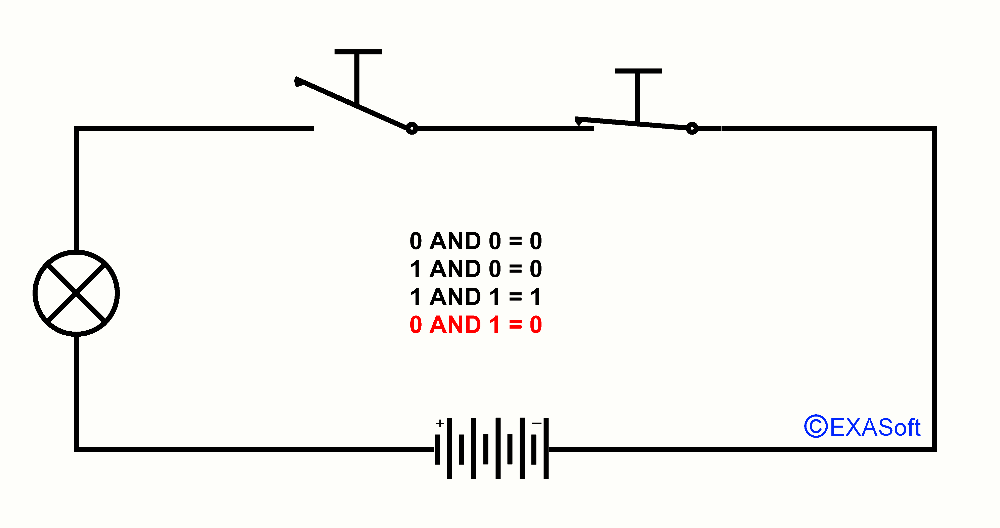
In this case, switch 1 AND switch 2 are pressed, the lamp switch on.
The table for AND is as follows:
0 AND 0 = 0
1 AND 0 = 0
0 AND 1 = 0
1 AND 1 = 1
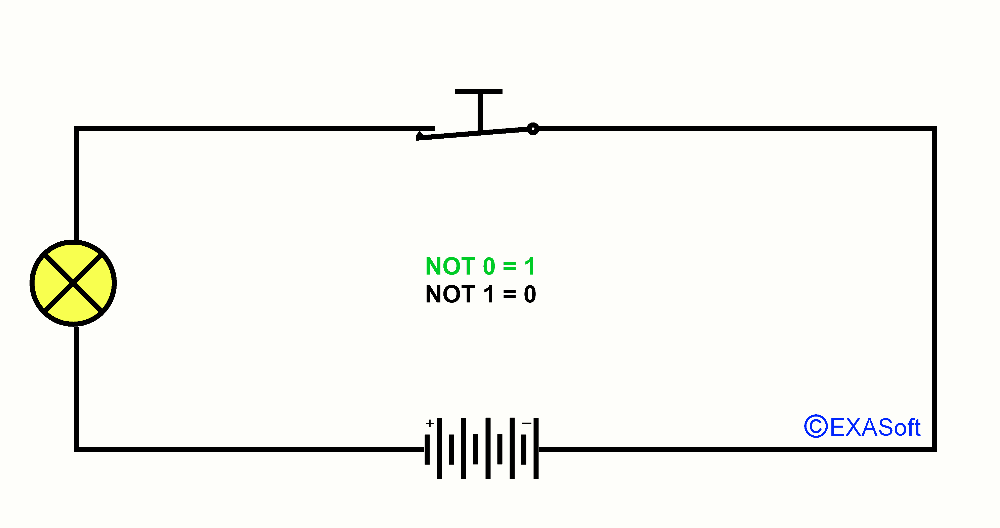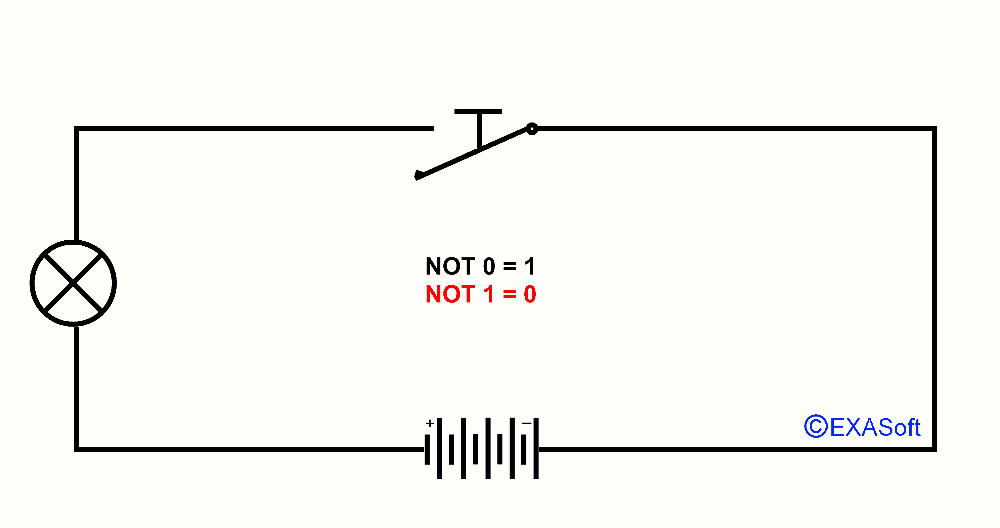
NOT Port
Then we have the NOT gate. Switch press means that he will:Not 1 = 0
Not 0 = 1
There are many possible combinations, for example the NAND and NOR port, a combination for Not AND and Not OR.
Here are some diagrams:
0 NAND 0 = 1 0 NOR 0 = 1
1 NAND 0 = 1 1 NOR 0 = 0
0 NAND 1 = 1 0 NOR 1 = 0
1 NAND 1 = 0 1 NOR 1 = 0
As you may have noticed the result is just the opposite of AND and OR.
XOR Port
So, now the essence of this page, XOR, XOR means "Exclusive OR". You could read it as "only OR applies to this switch". Just checkout the following picture: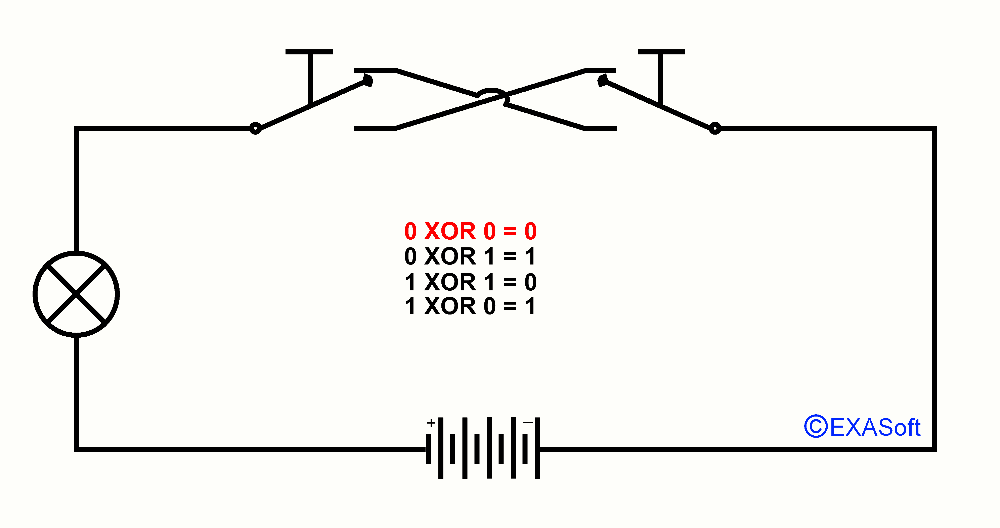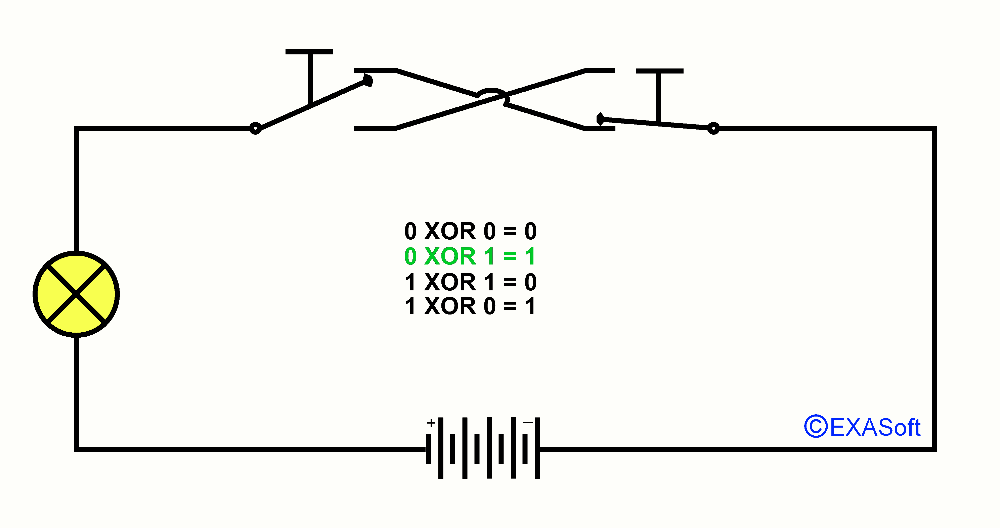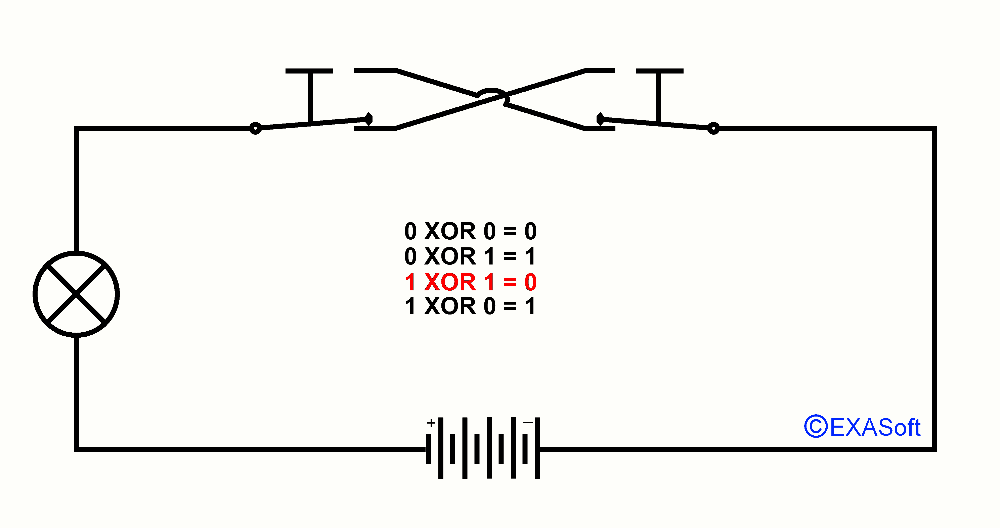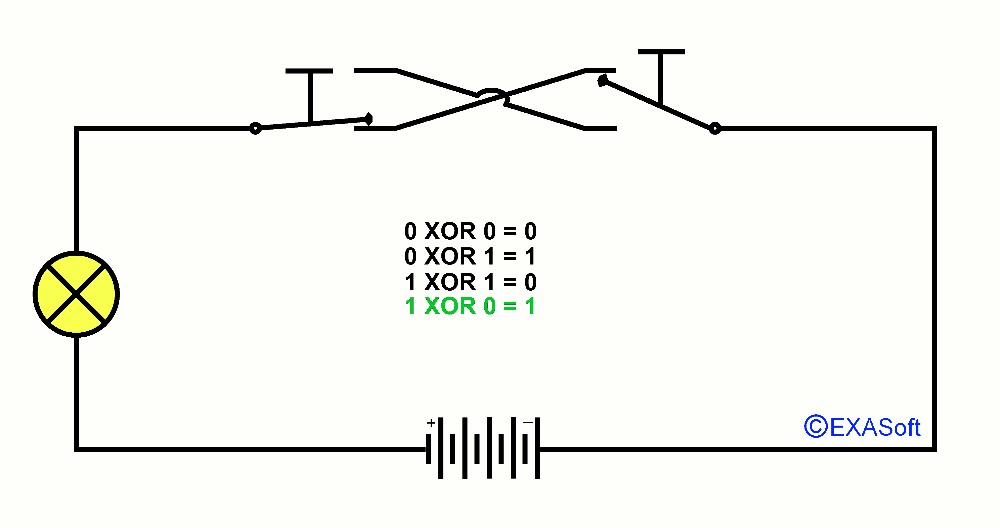
Here is the XOR table:
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 1 = 0
1 XOR 0 = 1
But what can we do with this?
Well lets say I have a series of Bits (binary digits) switches if you like
in this case 4 of them: 1100 (we call this the data)
And antoher series of bit's also 4 : 0101 (we call this the key, or password) if I XOR them with eachother you get this table:
1 XOR 0 = 1
1 XOR 1 = 0
0 XOR 0 = 0
0 XOR 1 = 1
Read this table from top to bottom on the left you see 1100 and just after the XOR's you see 0101
So !!?? If I XOR this, it will become a new series of bits: 1001 (This is the encrypted data)
I give you the encrypted data (1001) and the password (0101)
Lets XOR the encrypted series with the password series:
1001 was the encrypted series
0101 xor was the password
1100 (result)
See what happend? you got back the original data :)
Here first a small sample of the decimal number representing the binary number:
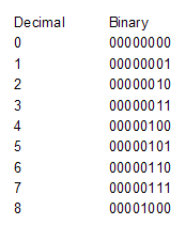
Now, before we go on you have to understand a bit about the ASCII table
Characters are encoded to a decimal number (A = 65 B = 66 etc ... Z=90) this is becourse computers do not understand anything else than bit's
If I take 65=”A” we can also write this binary. The binary system uses only 0 or 1, the kind of switches I explained. Binary 65 is 01000001, you can simply calculate the binary number when you put the decimals above them because every bit (binary digit) is the power of the previous one.

All switches on 11111111 = 128+64+32+16+8+4+2+1 = 255, along with 0, there are 256 possibilities.
Now I just have to add the "switched on" bits, in our case 64 +1 = “A” = 01000001
Now I will take another letter for example “Z”. “Z” = 90 = 01011010
When I put the binary’s of A and Z together and apply XOR the this you get this:
01000001
01011010 xor
00011011 and that’s decimal: 27.
So, I give you the number 27 and you should find out which characters I've used here? That’s not possible of course, because there are many possibilities that can cause 27.
But look what happens when I use 27 and XOR it with “Z” again:
00011011 = 27
01011010 = Z
01000001 ...
And what exactly was that again: 65 and thus “A”. So… if I have “Z” and XOR it with the encrypted data I can get back “A” again! Encrypting with a letter and encrypting again with the same letter leads to the original letter!
Here is something I made in excel to show you haw a complete word or sentence can be encrypted
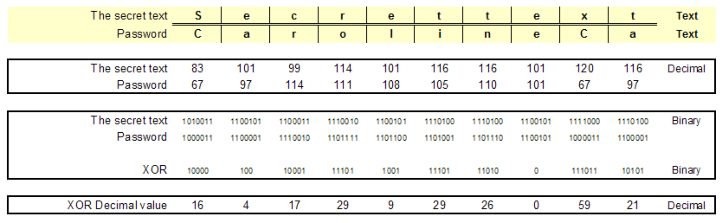
So you can see the encrypted values 16, 4, 17, 29, 9, 29, 26, 0, 59, 21 The "e" is 3 x in our secret encrypted text but in the encrypted data it is each time a different value because of the password. twice the number 29 appears in the encrypted text but the characters are not the same. So this text is realy encrypted and you can never trace back the original value. But if I have the password I can XOR the password to the encrypted text again

But how can I hack this? (hacking is the term for cracking passwords or text) Well, imagine that you do know the text but not the password:

At the bottom you see the password appear, so if you know the text, password protection is gone. This is why it is recomended to use a double XOR with a public key and a private key. I will not explain it here unless lots of people request me to do so, but the only thing happening is that you XOR the public password again with a private one and you do the same for decription, just XOR it twice. The ones and zeros can become very confusing so is there no better method to write this down? Sure there is, the hexadecimal (16-count) system. The hexadecimal system counts as follows:

Why is this useful, check out:

As you can see, the "decimals" of the hexadecimal system exactly match with the single bit values of the binary system.
So by heart I know that 255 decimal represents FF hexadecimal 256 = 100 (binary:100000000)
512 = 200 (1000000000)
1024 = 400 (10000000000)
Since we lose the overview of the binary system when we use more than 8 bits we groep them by eight (byte also means by eight)
Two bytes that belong together are called a word 11111111 11111111 = FF FF = 65535
Well this is enough for now, it is important to know and it can easy your work , but you should find out for yourselves if u find it use full. (Counting is still the easiest binary, even the computer can do it and there is nothing more stupid than that)
There are several methods to hack passwords, one of them called "Brute Force" Brute force is nothing more than trying all possibilities until you come across something that makes sense.
If you do that by hand can take a long time, but: We have a computer! A computer might be stupid, but it is fast also, it can easily test a 100,000 combinations per second.
So if we have a short password with only uppercase letters and only the A to Z, we have 26 * 26 * 26 = 17576 possibilities. By hand it would be impossible to check them all out, but for the computer to crack this it needs less than one second. The password will also will repeat, if I have the password ABC it will act like this: ABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABCABC
If I would use brute force to this I could use only the “A” to het 1/3 of the text correct. So I really only need 26 tests to perform and see what times 1 / 3 of the text looks good.
You see the repetitive pattern back when you try to hack.
But XOR Cryptology is still used, why? With long passwords which uses all characters it works fine, patterns are very difficult to find, if not impossible.
Let's say you have a password of 12 characters, upper and lower case and special characters and numbers. You then have 82^12 possibility’s = 92,420,056,270,299,900,000,000.
The computer would then take about 29,306,207,595 years to crack the code as it does 100,000 combinations per second. Big super computers are a lot faster, but it would still take at least 5,861,242 Year to crack this with brute force. Who sais its not safe enough?
We have now seen that brute force is really not an option for long complex passwords with XOR technology. How should we do it than? Search patterns, in many possible ways to find combinations. Try to capture them in an algorithm, and then we know what makes a cryptologist, pattern search, determine algorithms. What do we need to hack: preferably a very long text and a very short password. The shorter the encrypted text and the longer the password, the harder it is. But a very important thing for finding passwords and algorithms is this: What is the name of the owners wife, what are his children’s names , his pet, what year was he born, how does he usually choose his password. What keeps him busy. Can I install something on his computer to “catch” his password. 9 of 10 people who just have a new love, choose a password the name of their love, number combinations are often combinations of birth date or the date that they met or married. That and more can all be important factors for a real cryptologist. The next time I will explain RSA encrypion :) Do something with prime numbers Yeah nice!
